THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra giữa học kì 2 môn Toán 7 năm học 2022 – 2023 trường THCS Đức Giang, quận Long Biên, thành phố Hà Nội; đề thi gồm 02 trang, hình thức 30% trắc nghiệm + 70% tự luận, […]
Category Archives: ĐỀ THI GIỮA HK2 TOÁN 7
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra giữa học kì 2 môn Toán 7 năm học 2022 – 2023 trường THCS Ngọc Lâm, quận Long Biên, thành phố Hà Nội; đề thi mã đề T701 và mã đề T702 gồm 04 trang, cấu trúc […]
Tài liệu gồm 71 trang, tuyển tập 08 đề kiểm tra giữa học kì 2 môn Toán 7 Cánh Diều, các đề thi được biên soạn theo hình thức 30% trắc nghiệm + 70% tự luận, thời gian làm bài 90 phút, có khung ma trận, bảng đặc tả, đáp án và hướng dẫn chấm […]
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề thi giữa học kì 2 môn Toán 7 năm học 2023 – 2024 trường THCS Khương Thượng, thành phố Hà Nội; đề thi được biên soạn theo hình thức 20% trắc nghiệm + 80% tự luận, thời gian làm […]
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra giữa học kì 2 môn Toán 7 năm học 2023 – 2024 trường THCS Giảng Võ, quận Ba Đình, thành phố Hà Nội; kỳ thi được diễn ra vào ngày 13 tháng 03 năm 2024. Trích dẫn […]
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra giữa học kì 2 môn Toán 7 năm học 2023 – 2024 trường TH&THCS Ngôi Sao Hà Nội, thành phố Hà Nội; đề thi gồm 02 trang, hình thức 20% trắc nghiệm (08 câu) + 80% tự […]
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra giữa học kì 2 môn Toán 7 năm học 2023 – 2024 trường THCS Song Mai, thành phố Bắc Giang, tỉnh Bắc Giang; đề thi có đáp án trắc nghiệm và hướng dẫn chấm điểm tự luận. […]
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra chất lượng giữa học kỳ 2 môn Toán 7 năm học 2023 – 2024 trường THCS Giao Long, huyện Giao Thủy, tỉnh Nam Định; đề thi có đáp án trắc nghiệm và hướng dẫn chấm điểm tự […]
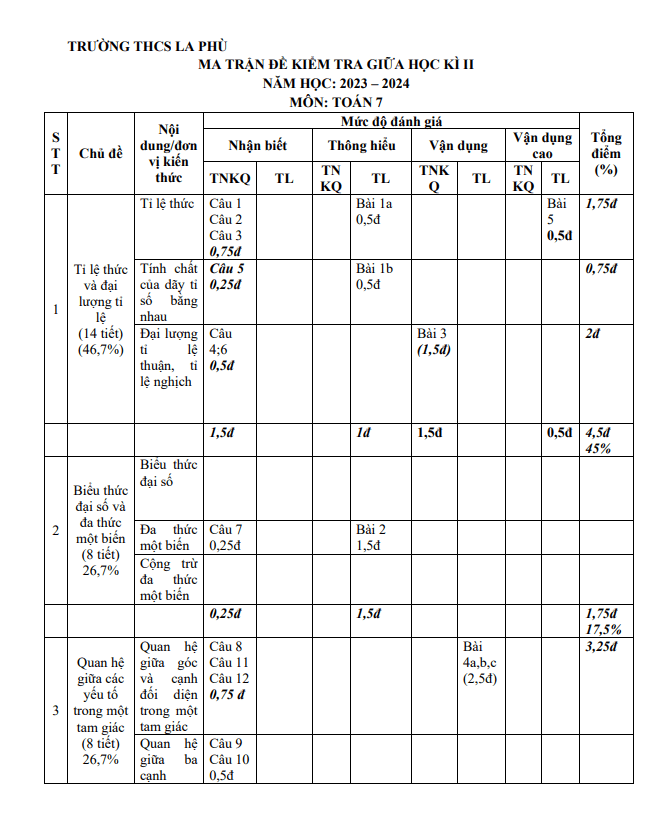
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề kiểm tra giữa học kỳ 2 môn Toán 7 năm học 2023 – 2024 trường THCS La Phù, thành phố Hà Nội; đề thi có đáp án và hướng dẫn chấm điểm. Trích dẫn Đề giữa học kỳ 2 […]
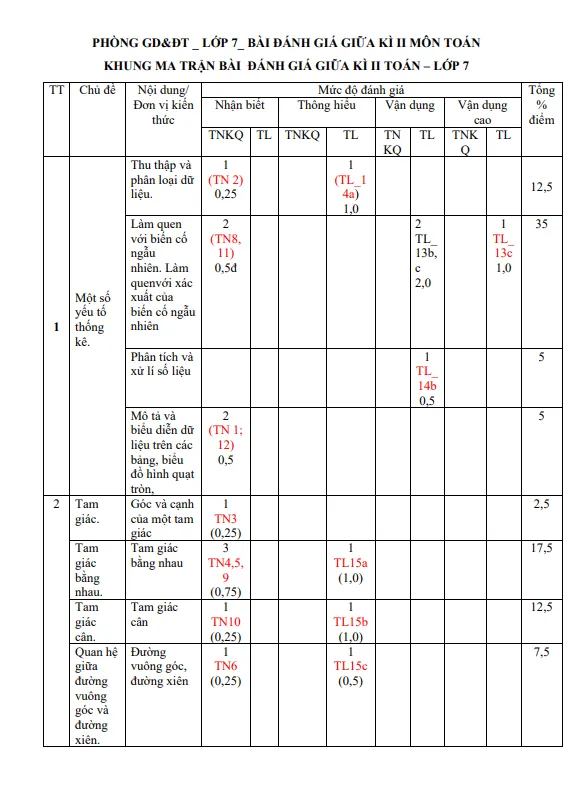
THCS.TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề khảo sát chất lượng giữa học kì 2 môn Toán 7 THCS năm học 2023 – 2024 phòng Giáo dục và Đào tạo huyện Giao Thuỷ, tỉnh Nam Định; đề thi gồm 02 trang, hình thức 30% trắc nghiệm […]