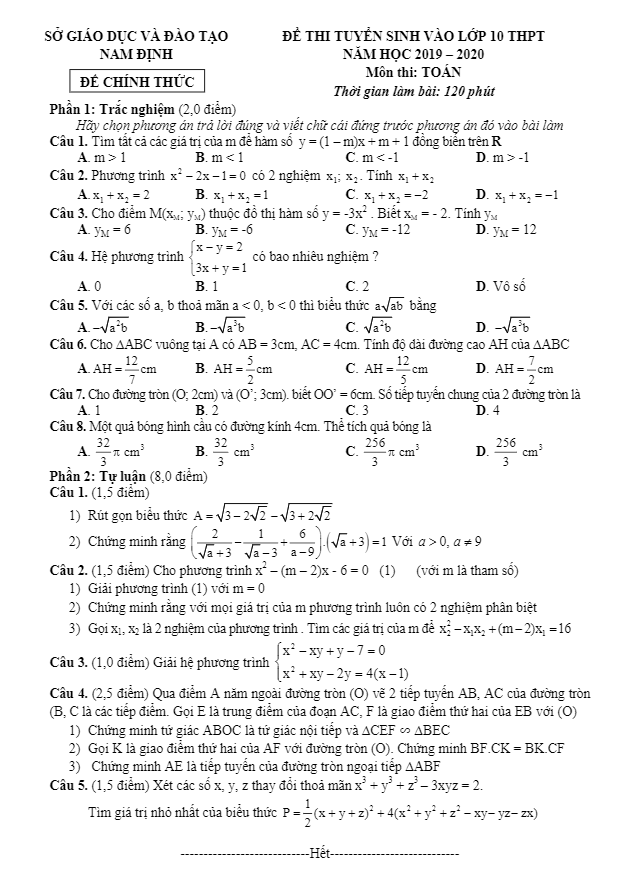Nhằm tuyển chọn các em học sinh đã tốt nghiệp khối Trung học Cơ sở, đáp ứng đủ năng lực học tập, vào học tại các trường Trung học Phổ thông trên địa bàn tỉnh Nam Định, vừa qua, sở Giáo dục và Đào tạo tỉnh Nam Định đã tổ chức kỳ thi Toán tuyển sinh lớp 10 THPT năm học 2019 – 2020.
Bạn đang đọc: Đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Nam Định
Đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Nam Định được biên soạn theo dạng trắc nghiệm khách quan kết hợp với tự luận, đề thi gồm 01 trang, phần trắc nghiệm gồm 8 câu, chiếm 20% số điểm, phần tự luận gồm 05 câu, chiếm 80% số điểm, thời gian học sinh làm bài là 120 phút, đề thi có đáp án và lời giải chi tiết.
Trích dẫn đề tuyển sinh lớp 10 THPT năm 2019 – 2020 môn Toán sở GD&ĐT Nam Định:
+ Qua điểm A năm ngoài đường tròn (O) vẽ 2 tiếp tuyến AB, AC của đường tròn (B, C là các tiếp điểm. Gọi E là trung điểm của đoạn AC, F là giao điểm thứ hai của EB với (O).
1) Chứng minh tứ giác ABOC là tứ giác nội tiếp và ∆CEF đồng dạng ∆BEC.
2) Gọi K là giao điểm thứ hai của AF với đường tròn (O). Chứng minh BF.CK = BK.CF.
3) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp ∆ABF.
+ Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm: Tìm tất cả các giá trị của m để hàm số y = (1 – m)x + m + 1 đồng biến trên R.
+ Xét các số x, y, z thay đổi thoả mãn x^3 + y^3 + z^3 – 3xyz = 2. Tìm giá trị nhỏ nhất của biểu thức P = 1/2.(x + y + z)^2 + 4(x^2 + y^2 + z^2 – xy – yz – zx).