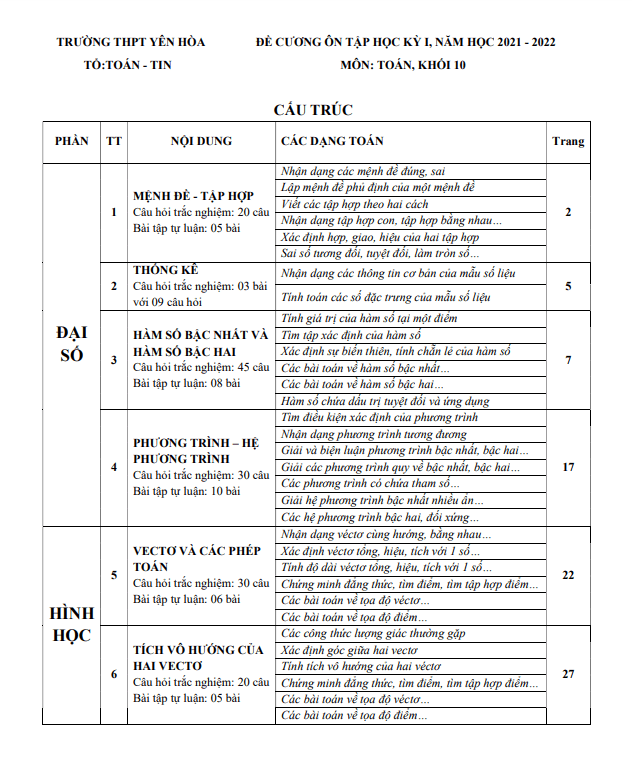
TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp lớp 10 đề cương ôn tập học kỳ 1 Toán 10 năm học 2021 – 2022 trường THPT Yên Hòa – Hà Nội.
Bạn đang đọc: Đề cương ôn tập học kỳ 1 Toán 10 năm 2021 – 2022 trường THPT Yên Hòa – Hà Nội
PHẦN I: ĐẠI SỐ.
CHƯƠNG 1: MỆNH ĐỀ – TẬP HỢP.
1. Kiến thức
– Trình bày được định nghĩa mệnh đề, mệnh đề phủ định, mệnh đề kéo theo, mệnh đề đảo, mệnh đề tương đương, khái niệm mệnh đề chứa biến và nêu được ý nghĩa kí hiệu.
– Trình bày được khái niệm tập hợp, tập con, hai tập hợp bằng nhau, các tập con của tập R.
– Trình bày được khái niệm số gần đúng, sai số, số quy tròn.
2. Kỹ năng
– Xác định được tính đúng sai của mệnh đề. Biết lập mệnh đề đảo của một mệnh đề cho trước. Phân biệt được giả thiết và kết luận. Biết sử dụng thuật ngữ: điều kiện cần, điều kiện đủ, điều kiện cần và điều kiện đủ.
– Sử dụng đúng các kí hiệu. Biểu diễn được tập hợp bằng các cách: liệt kê hoặc chỉ ra tính chất đặc trưng. Thực hiện thành thạo các phép toán lấy giao, hợp của hai tập hợp, phần bù của một tập hợp trong tập hợp khác.
– Viết được số quy tròn của một số căn cứ vào độ chính xác cho trước, Biết sử dụng máy tính bỏ túi để tính toán các số gần đúng.
CHƯƠNG 2: THỐNG KÊ.
1. Kiến thức
– Mô tả được mẫu số liệu, phân biệt được số trung bình, số trung vị, phương sai và độ lệch chuẩn.
2. Kỹ năng
– Đọc được tần số, tần suất, mốt của một mẫu số liệu. Đọc và vẽ được các biểu đồ tần số, tần suất.
– Vận dụng được công thức tính số trung bình, số trung vị, phương sai và độ lệch chuẩn vào bài tập thực tế.
CHƯƠNG 3: HÀM SỐ BẬC NHẤT – HÀM SỐ BẬC HAI.
1. Kiến thức
– Trình bày được khái niệm hàm số, tập xác định của hàm số, đồ thị của hàm số, hàm số đồng biến, nghịch biến, hàm số chẵn, lẻ. Minh họa được tính chất đồ thị của hàm số chẵn, lẻ. Nêu được các phép tịnh tiến đồ thị.
– Trình bày được bảng biến thiên và đồ thị của hàm số bậc nhất. Cách vẽ đồ thị hàm số bậc nhất và đồ thị hàm số chứa dấu trị tuyệt đối.
– Trình bày được sự biến thiên của hàm số bậc hai. Giải thích được phép tịnh tiến đồ thị để có ĐTHS bậc hai. Cách vẽ đồ thị hàm số bậc hai.
2. Kỹ năng
– Tìm được tập xác định của hàm số. Xét được tính đồng biến, nghịch biến của một số hàm số trên một khoảng cho trước, xét được tính chẵn lẻ của một hàm số. Vẽ được đồ thị hàm số mới khi sử dụng phép tịnh tiến đồ thị.
– Xác định được chiều biến thiên và vẽ đồ thị của hàm số bậc nhất và đồ thị hàm số chứa dấu trị tuyệt đối. Tìm toạ độ giao điểm của hai đường thẳng có phương trình cho trước. Khảo sát sự biến thiên và vẽ đồ thị của hàm số cho bởi các hàm bậc nhất trên các khoảng khác nhau.
– Lập được bảng biến thiên của hàm số bậc hai. Vẽ được đồ thị hàm số bậc hai, xác định được: trục đối xứng của đồ thị, các giá trị của x để y > 0, y CHƯƠNG 4: PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH.
1. Kiến thức
– Trình bày được khái niệm phương trình, phương trình có tham số, phương trình nhiều ẩn, nghiệm của phương trình, hai phương trình tương đương, các phép biến đổi tương đương.
– Trình bày được cách giải và biện luận phương trình dạng.
– Trình bày được cách giải một số phương trình quy về dạng, phương trình có ẩn ở mẫu thức, chứa dấu giá trị tuyệt đối, phương trình đưa về phương trình tích.
– Trình bày được khái niệm nghiệm phương trình bậc nhất hai ẩn và hệ phương trình bậc nhất hai ẩn, các dạng hệ phương trình bậc hai hai ẩn.
2. Kỹ năng
– Nhận biết một số là nghiệm của phương trình, nhận biết hai phương trình tương đương. Tìm điều kiện xác định của phương trình, biến đổi tương đương phương trình.
– Áp dụng cách giải và biện luận phương trình dạng vào làm bài tập. Biết sử dụng định lí Viet tìm tham số để phương trình thỏa mãn điều kiện cho trước.
– Biến đổi bài toán để đưa về các dạng được học: phương trình bậc nhất, bậc hai, phương trình có ẩn ở mẫu thức, phương trình có chứa dấu giá trị tuyệt đối, phương trình đưa về phương trình tích. Áp dụng vào giải các bài toán thực tế.
– Giải và biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn. Giải và biện luận hệ phương trình bậc nhất hai ẩn bằng định thức. Giải một số hệ phương trình bậc hai hai ẩn: hệ gồm một phương trình bậc hai và một phương trình bậc nhất, hệ phương trình đối xứng, hệ giải bằng phương pháp phân tích thành nhân tử.
PHẦN II: HÌNH HỌC.
CHƯƠNG 1: CÁC PHÉP TOÁN VECTƠ.
1. Kiến thức
– Trình bày được khái niệm vectơ, vectơ không, độ dài vectơ, hai vectơ cùng phương, hai vectơ bằng nhau.
– Trình bày được cách xác định tổng, hiệu hai vectơ, quy tắc ba điểm, quy tắc hình bình hành và các tính chất của tổng vectơ: giao hoán, kết hợp, tính chất của vectơ không.
– Trình bày được định nghĩa và các tính chất của tích vectơ với một số. Tính chất trung điểm, trọng tâm; điều kiện để hai vectơ cùng phương, ba điểm thẳng hàng, biểu thị một vectơ theo hai vectơ không cùng phương.
– Trình bày được định nghĩa toạ độ của vectơ và của điểm đối với một hệ trục toạ độ. Các biểu thức toạ độ của các phép toán vectơ, toạ độ trung điểm của đoạn thẳng và toạ độ trọng tâm của tam giác.
2. Kỹ năng
– Chứng minh hai vectơ bằng nhau. Cho điểm A và vectơ a, dựng được điểm B để AB a.
– Vận dụng quy tắc ba điểm, quy tắc hình bình hành, quy tắc trừ khi lấy tổng, hiệu hai vectơ cho trước và chứng minh các đẳng thức vectơ.
– Xác định được b = k.a. Diễn đạt được bằng ngôn ngữ vectơ: ba điểm thẳng hàng, trung điểm của một đoạn thẳng, trọng tâm của tam giác, hai điểm trùng nhau. Sử dụng được tính chất trung điểm của đoạn thẳng, trọng tâm của tam giác để giải một số bài toán hình học.
– Tính được toạ độ của vectơ nếu biết toạ độ hai đầu mút. Sử dụng được biểu thức toạ độ của của các phép toán vectơ trong các bài toán. Xác định được toạ độ trung điểm của đoạn thẳng, toạ độ trọng tâm tam giác.
CHƯƠNG 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ.
1. Kiến thức
– Trình bày được định nghĩa tỉ số lượng giác của góc bất kì từ đến 18 và nhớ được giá trị lượng giác của một số góc đặc biệt.
– Trình bày được khái niệm góc giữa hai vectơ, tích vô hướng của hai vectơ, các tính chất tích vô hướng, biểu thức toạ độ của tích vô hướng.
2. Kỹ năng
– Áp dụng quy tắc tìm GTLG của các góc tù bằng cách đưa về GTLG của các góc nhọn.
– Xác định được góc giữa hai vectơ. Vận dụng được các tính chất của tích vô hướng của hai vectơ trong tính toán, chứng minh đẳng thức, tìm tập hợp điểm thỏa mãn tính chất.